
技術文章
TECHNICAL ARTICLES 更新時間:2025-11-17
更新時間:2025-11-17 點擊次數:41
點擊次數:41
如何為精密設備“隔離"振動?——深入解析被動隔振原理與關鍵參數
在前期內容中,我們已認識到振動對精密設備的 “隱形傷害",并掌握通過 VC 曲線開展 “環境體檢" 的方法。當振動問題浮現,被動隔振作為應用zui廣泛的解決方案,憑借無需外部能量、成本低、可靠性高的優勢,成為多數精密設備的shou選。本文將聚焦被動隔振,系統拆解其物理本質、核心原理、設計邏輯與性能評估標準,為被動隔振方案的選型與設計提供理論支撐。
一、 隔振的本質:打造一個安靜的“微環境"
隔振的核心目標并非消除所有振動 —— 現實中無法實現,而是在振動源頭(如地面、設備周邊環境)與受保護的精密設備之間,構建一個 “振動過濾器"。該過濾器通過改變振動能量的傳遞路徑與效率,大幅衰減傳遞至設備的振動能量,將振動影響控制在設備允許的精度范圍內,最終保障設備運行精度、數據可靠性與使用壽命,為設備創造相對靜止的 “微環境"。
以半導體行業 7 納米芯片光刻工藝為例,光刻機工作臺需在納米級精度下完成移動。若地面傳遞 0.01 毫米(約頭發絲直徑 1/5)的振動,會直接導致光刻圖案偏移,造成晶圓報廢。此時,被動隔振技術需將外界振動對工作臺的影響控制在 “亞納米級",通過彈性與阻尼元件的協同作用,為光刻過程構建 “振動可忽略" 的穩定環境,這正是被動隔振本質的典型體現。
二、被動隔振核心概念與關鍵性能參數
理解被動隔振的基礎是掌握其核心概念與性能指標,這是后續原理分析與設計的前提。
1、基礎概念定義與作用
概念 | 定義 | 核心作用 |
振動傳遞率(T) | 受保護對象的振動響應(幅值 / 加速度)與激勵源振動輸入的比值(無量綱) | 直接衡量隔振效果,T 越小隔振效果越好(理想值趨近于 0) |
固有頻率(f0) | 被動隔振系統(彈性元件 + 被隔振質量)自由振動時的固有頻率(單位:Hz) | 決定被動隔振的 “有效隔振區" 起點,僅當激勵頻率 f> f0時被動隔振才起效,f0越低,有效隔振區覆蓋的頻率范圍越廣 |
阻尼比() | 系統實際阻尼與 “臨界阻尼" 的比值(無量綱),反映能量耗散能力 | 1. 抑制共振峰值:當激勵頻率接近 f?(頻率比 r≈1)時,ζ 越大,共振幅值越小; 2. 影響有效隔振效果:ζ 越大,有效隔振區的 T 值越大,隔振效率越低,需權衡共振抑制與隔振性能 |
品質因子(Q) | 反映系統共振尖銳程度的參數,與阻尼比的關系為 ζ=1/(2Q)(無量綱) | 間接體現阻尼水平:Q 越大,阻尼越小,共振峰值越高,但有效隔振區效果越好;Q 越小,阻尼越大,共振峰值越低,但有效隔振效果越弱 |
剛度(k) | 彈性元件產生單位位移所需的力(單位:N/m),計算公式為 k=F/Δx(F 為作用力,Δx 為位移) | 決定系統固有頻率:被隔振質量固定時,k 越小(彈性元件越 “軟"),f?越低 |
2. 關鍵性能參數解析
l 隔振效率(η):與振動傳遞率互補,計算公式為 η=(1-T)×100%。例如,當 T=0.2 時,η=80%,表示 80% 的振動能量被隔離,僅 20% 傳遞至設備,直觀反映被動隔振系統的能量衰減能力。
l 共振峰值(Tmax):被動隔振系統在共振點(r=1,即激勵頻率 = 固有頻率)時的最大傳遞率。忽略阻尼時,Tmax趨近于無窮大;實際應用中,需通過合理設計阻尼,將 Tmax控制在<5 的安全范圍,避免共振導致設備結構損壞或精度失效。
l 頻率響應范圍:被動隔振系統有效工作的頻率區間, f> f0的頻段。例如,若系統
f?=2Hz,有效隔振范圍為 f>2.828Hz,無法對 2.828Hz 以下的低頻振動起到隔離作用,這是被動隔振的固有特性。
三、被動隔振(Passive Vibration Isolation)核心原理:單自由度質量 - 彈簧 - 阻尼系統
被動隔振是zui常用的隔振方式,無需外部能量輸入,僅通過彈性元件(如彈簧、橡膠)、阻尼元件(如阻尼器)構成的系統改變振動傳遞特性。
最基礎且最重要的理論模型是單自由度質量-彈簧-阻尼系統(圖1)。它抽象地描述了被動隔振系統的核心物理特性,是所有復雜隔振器設計的理論基石。
1、系統模型構成
該系統是理解被動隔振的基礎模型,包含三個基本元素:
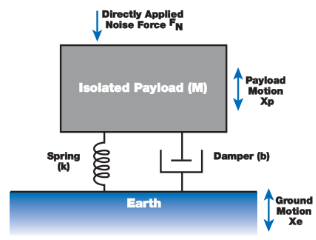
圖1
l 被隔離的質量塊(M:被隔振負載的質量): 代表需要被隔離的負載,在此處被簡化為一個無內部共振的單質量塊(單位:kg)。
l 彈簧(k:彈簧的剛度): 代表隔振器的彈性支撐元件(如TMC氣動隔振器中的空氣彈簧),作用是支撐負載,并對負載施加一個力,該力由以下公式給出:
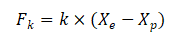
其中![]() 和
和![]() 和分別代表地面(振源)和負載的動態位置;彈簧剛度 k 越小,系統固有頻率 f?越低,越容易進入有效隔振區。
和分別代表地面(振源)和負載的動態位置;彈簧剛度 k 越小,系統固有頻率 f?越低,越容易進入有效隔振區。
l 阻尼器(b:阻尼系數):代表消耗振動能量的元件如TMC Gimbal Piston中的阻尼孔、MaxDamp中的阻尼油),通過將質量塊的動能轉化為熱量(如阻尼孔中流體的摩擦熱)實現能量耗散,最終使系統恢復靜止。這是通過產生一個與負載相對于地面的速度成正比且方向相反的力來實現的:

從力學公式可見,兩個方程中都存在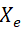 ,地面振動通過彈簧與阻尼器以力的形式傳遞至被隔離質量塊,被動隔振的核心就是通過調整 k、b、M 的參數,改變振動傳遞效率,實現 “過濾" 振動的目標。
,地面振動通過彈簧與阻尼器以力的形式傳遞至被隔離質量塊,被動隔振的核心就是通過調整 k、b、M 的參數,改變振動傳遞效率,實現 “過濾" 振動的目標。
2、 振動傳遞率公式與曲線特征
通常,我們不使用參數M,k,b和來描述系統,而是定義一組新的參數,這些參數能更直接地與質量-彈簧系統的可觀測特性相關聯。
第一個是固有頻率:

它描述了在沒有任何阻尼(b=0)的情況下,系統自由振蕩的頻率。通常使用以下兩個常見參數之一來描述系統中的阻尼:品質因子Q和阻尼比ζ

這個理想化系統的傳遞率為:
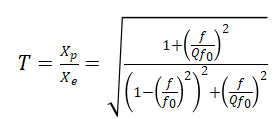 (1)
(1)
下圖繪制了對于幾個不同的品質因子Q,系統傳遞率隨頻率比變化的曲線。所繪制的Q值范圍從0.5到100。Q=0.5的情況是一個特例,稱為臨界阻尼,是指當系統發生位移后釋放時,不會超過平衡位置的阻尼水平。阻尼比就是系統阻尼與臨界阻尼的比值。我們使用Q而不是ζ,是因為因為對于Q 大于約2的情況下,在ω=ω0的時候,T≈Q。(其中ω和ω0為角頻率,ω=2πf)。

圖2
不同 Q 值(阻尼水平)的系統,傳遞率隨頻率比 r(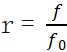 ,f為激勵頻率,f0為固有頻率) 的變化呈現明確規律,可分為三個階段
,f為激勵頻率,f0為固有頻率) 的變化呈現明確規律,可分為三個階段
l 同步振動段(r<1,即 f<f?):T≈1,被隔離質量塊隨地面同步運動,彈簧與阻尼器無法起到隔振作用。例如,當地面振動頻率為 1Hz,系統 f?=2Hz 時,設備會跟隨地面 1Hz 的振動同步晃動,無隔振效果。
l 共振危險段(r≈1,即 f≈f?):T>1,振動被放大,放大倍數約等于 Q 值(Q 越大,共振峰值越高)。若此時 Tmax>5,可能導致設備結構變形或精度失效,需通過增大阻尼(減小 Q)降低共振峰值。
l 有效隔振段(r>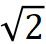 ,即 f>
,即 f> f?):這是隔振器發揮作用的區域。T 隨 r2 的增大而減小,隔振效果逐漸增強。此時阻尼越小(Q 越大),T 值越小,隔振效果越好。可見低阻尼在有效隔振段更具優勢。
f?):這是隔振器發揮作用的區域。T 隨 r2 的增大而減小,隔振效果逐漸增強。此時阻尼越小(Q 越大),T 值越小,隔振效果越好。可見低阻尼在有效隔振段更具優勢。
這一曲線清晰揭示了被動隔振的核心矛盾:阻尼增大可抑制共振,但會削弱有效隔振效果;阻尼減小能提升有效隔振效果,但會加劇共振風險,設計時需根據實際場景平衡二者關系。
直接施加在負載上的力傳遞到負載的運動幅值,其形式與公式1表達的略有不同。這個傳遞函數具有單位力引起的位移的量綱(如 m/N),因此不應與(無量綱的)傳遞率混淆:

下圖繪制了此函數隨頻率變化的曲線,降低 Q 值會在所有頻率減小負載的響應。
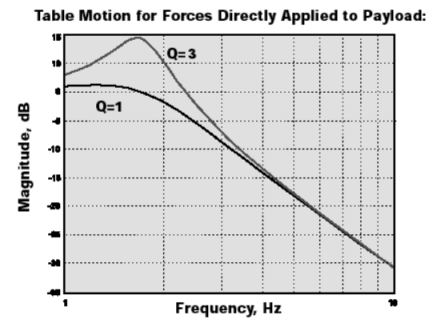
圖3
TMC的MaxDamp®隔振器正是利用了這一特性,適用于主要擾動產生于被隔振負載本身的應用。圖4顯示了與圖3中曲線相對應的負載的時域響應。該圖也說明了系統一旦受到擾動后的衰減情況。衰減的包絡線為 ![]() 。
。
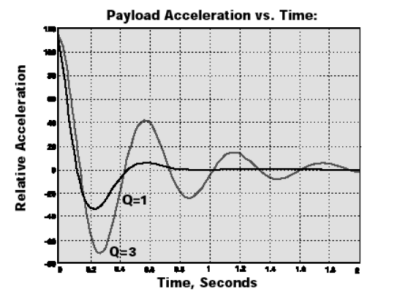
圖4
實際系統與圖1所示的簡單模型存在一些顯著差異,最重要的一點是實際系統具有六個運動自由度((DOF)。這些自由度并非獨立,在大多數系統中存在強烈的耦合。例如,“水平傳遞函數"通常顯示兩個共振峰,因為負載的水平運動會引起傾斜運動,反之亦然。
四、 隔振器的設計目標、思路與關鍵權衡
(一)核心設計目標
被動隔振器的設計核心是 “匹配固有頻率 f?與阻尼比 ζ",實現兩大目標:
(1) 確保系統能進入有效隔振區(r>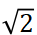 ),即讓設備實際面臨的主要振動頻率 f>
),即讓設備實際面臨的主要振動頻率 f>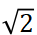 f0
f0
(2) 將共振峰值控制在安全范圍,避免共振對設備造成損害。
因此,隔振器最核心的設計目標非常明確。根據固有頻率公式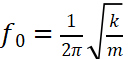 ,降低 f?是擴大有效隔振區的關鍵 ——f?越低,有效隔振區的起始頻率(
,降低 f?是擴大有效隔振區的關鍵 ——f?越低,有效隔振區的起始頻率( f0)越低,能覆蓋更多低頻振動場景(如地面常見的 2-10Hz 振動)。其中:k是隔振器的剛度(越“軟"越好)m是隔振器所承載的質量(越“重"越好)。
f0)越低,能覆蓋更多低頻振動場景(如地面常見的 2-10Hz 振動)。其中:k是隔振器的剛度(越“軟"越好)m是隔振器所承載的質量(越“重"越好)。
(二)具體設計思路
設計思路因此清晰,降低 f?主要有兩大途徑:
1. 降低彈性元件剛度 k選用 “更軟" 的彈性元件,減少單位位移所需的力,從而降低系統剛度。例如:
TMC 氣浮隔振器利用壓縮空氣的低剛度特性,垂直剛度可低至 10N/m 以下,使系統 f?降至 1.5-2.0Hz;
橡膠隔振器通過選用低硬度橡膠材料(如邵氏硬度 30-50 度),降低剛度,適用于中低頻振動隔離。
2. 增加被隔離質量 M,在彈性元件剛度固定時,增大被隔離質量可直接降低 f?。
例如:
精密光學設備常用 500-1000kg 的花崗巖平臺作為底座,通過增大 M,配合空氣彈簧的低 k 值,使系統 f?降至 2Hz 以下;
半導體檢測設備通過加裝鑄鐵配重塊(質量可達 200kg 以上),提升系統穩定性的同時,降低 f?。關鍵權衡:“隔振性能" vs “系統穩定性"
(三) 關鍵設計權衡
被動隔振設計中存在兩大核心權衡,需根據設備場景靈活調整:
1、 “低 f?" 與 “靜態穩定性" 的權衡
系統越 “軟"(k 越小,f?越低),隔振效果越好,但受擾動后(如人員走動、設備內部運動)的恢復時間越長,靜態穩定性越差。例如,f?=1Hz 的系統受擾動后,恢復至靜止狀態需 5-10 秒;而 f?=5Hz 的系統恢復時間僅需 0.5-1 秒。
優化方案:控制靜態沉降量 ,同時通過優化設備重心(如降低重心高度),提升抗傾覆能力。
2、 “共振抑制" 與 “有效隔振" 的權衡
增大阻尼(ζ 增大)可降低共振峰值,但會導致有效隔振區的 T 值增大,隔振效率下降;減小阻尼(ζ 減小)能提升有效隔振效率,但會使共振峰值升高。
優化方案:根據激勵頻率與 f?的比值 r 調整 ζ:
若 r>3(激勵頻率遠離 f?,共振風險低):取小阻尼(ζ=0.05-0.1),優先保證有效隔振效果;
若 r=1.5-2(激勵頻率接近 f?,共振風險高):取大阻尼(ζ=0.2-0.3),優先抑制共振峰值。
五、 被動隔振設計常見誤區與優化方向
在被動隔振方案設計與選型中,易因對原理理解不深入導致效果不佳,以下是三大常見誤區及優化建議:
誤區 1:盲目追求低固有頻率 f?
問題:過度降低 f?會導致靜態沉降量 δst 大幅增大,可能引發高重心設備(如立式光刻機)傾覆,或使彈性元件(如彈簧)因過度壓縮而永jiu損壞;同時,過低的 f?會延長系統擾動恢復時間,影響設備動態穩定性。
優化方向:根據設備使用場景設定合理 f?:
低頻振動環境(如實驗室地面 2-5Hz 振動):f?控制在 1.5-2.5Hz,確保 f?<2Hz,覆蓋低頻振動;
f?<2Hz,覆蓋低頻振動;
中高頻振動環境(如工廠車間 10-50Hz 振動):f?控制在 3-5Hz,平衡穩定性與隔振效果;嚴格控制靜態沉降量,避免調平困難。
誤區 2:忽視阻尼的雙重作用,過度增減阻尼
問題:部分設計中為追求 “ji致隔振",過度減小阻尼(ζ<0.05),導致共振峰值 Tmax>5,設備在共振頻率下運行時精度嚴重受損;或為 “避免共振",過度增大阻尼(ζ>0.3),使有效隔振區 T 值>0.3(隔振效率<70%),無法滿足精密設備需求。
優化方向:基于激勵頻率分布調整阻尼:
先通過 VC 曲線檢測環境振動頻率,確定主要振動頻率 f 與系統 f?的比值 r;
若 r>3,選 ζ=0.05-0.1(如氣浮隔振器搭配低阻尼阻尼器);
誤區 3:彈性元件與負載不匹配,剛度或承載能力失衡
問題:彈性元件選型時,未根據 “設備重量 + 底座重量" 精確匹配剛度與承載能力:
剛度過高(k 過大):導致 f?過高,有效隔振區起始頻率 f?>主要振動頻率,無隔振效果;
f?>主要振動頻率,無隔振效果;
承載能力不足(彈性元件額定負載<實際負載):彈性元件yong久變形,剛度失效;
承載能力過剩(額定負載遠大于實際負載):彈性元件形變量過小,無法起到 “軟支撐" 作用,f?偏高。
優化方向:精確計算總負載 Mtotal = 設備重量 + 底座重量,根據 f?目標值,通過公式![]() 計算所需剛度;選擇彈性元件時,確保其額定負載為 Mtotal 的 1.2-1.5 倍,避免超載或負載不足;
計算所需剛度;選擇彈性元件時,確保其額定負載為 Mtotal 的 1.2-1.5 倍,避免超載或負載不足;
多支點隔振(如 4 個隔振器支撐設備)時,需保證各支點負載均勻,避免彈性元件受力不均導致剛度偏差。
六、 總結與TMC的實踐
隔振并非 “越嚴格越好",而是需要基于 VC 曲線評估結果,結合實驗精度需求、環境振動特性,選擇方案。TMC 的隔振技術之所以能在全球精密領域廣泛應用,核心在于其始終以 “理論為基、場景為導向"—— 從經典的Gimbal Piston™氣浮隔振器到高阻尼的MaxDamp®系列,其設計都嚴格遵循這些基礎原理,并在工程上做到了ji致,為客戶在不同應用場景下提供隔振解決方案。
下一篇內容,我們將進一步聚焦 TMC 被動隔振產品的具體結構設計、參數選型方法及典型行業應用案例,幫助大家更好地掌握被動隔振方案的選型與應用,敬請期待!
---
公司郵箱: panyue@sourcescn.com
服務熱線: 0532-80982936
公司地址: 山東省青島市黃島區峨眉山路396號光谷軟件園57號樓501
Copyright © 2025 青島森泉光電有限公司 All Rights Reserved
備案號:魯ICP備18050584號-2
技術支持:化工儀器網 管理登錄 sitemap.xml
